Learn Math: Desember 2016

Selasa, 20 Desember 2016

Metode Posisi Palsu
Algoritma penyelesaian :
1. ambil a1 = a dan b1 = b
2. untuk n = 1, 2, 3, ...

$p_n = b_n - \frac{f(b_n)(b_n - a_n)}{f(bn)-f(a_n)}$
jika $f(a_n)f(b_n)< 0$ maka

Menentukan Akar-akar Persamaan Nonlinear ( Metode Numerik )

Beberapa metode yang dapat digunakan untuk menentukan akar-akar persamaan non linear adalah sebagai berikut :
Metode tertutup
- Metode bagi dua (biseksi)
- Metode posisi palsu
Metode Terbuka
- Metode Newton Raphson
- Metode Secant

Yang pertama yang akan di bahas adalah :
- Metode Bagi 2 (Biseksi)
Algoritma (langkah-langkah penyelesaiannya) :
1. ambillah a1 = a dan b1 = b
2. untuk n = 1, 2, 3, ...
$p_n = an + \frac{b_n - a_n}{2}$
Jika $f_{(a_n)}f_{(p_n)} < 0$ maka $a_{n+1} = an , b_{n+1}= P_n$
Jika $f_{(a_n)}f_{(p_n)}> 0$ maka $a_{n+1}=p_n , b_{n+1}=b_n$

nilai a dan b dapat ditentukan dengan sembarang nilai dengan syarat $f(a) \times f(b) < 0$ maka a dan b dapat digunakan.

Iterasi dapat dilakukan terus hingga didapatkan nilai akar-akar persamaan non linear. iterasi dapat berakhir ketika nilai

$f(p) < 0.001$

Senin, 19 Desember 2016

Turunan Numerik [ Metode Numerik ]

Turunan Numerik
Turunan fungsi dapat didefinisikan
$f'(x) =\lim_{x\rightarrow 0} \frac{f(x+h)-f(x))}{h}$
Terdapat tiga pendekatan untuk menghitung $f'(x_0)$ :
1. Selisih Maju
dapat di rumuskan dengan :
$f'(x_0)=\frac{f(x_0) - f(x_0 - h)- }{h} = f_0 - \frac{f_1}{h}$ $f'(x_0)=\frac{f(x_0 + h)- f(x_0)}{h} = \frac{f_1-f_0}{h}$
2. Selisih Mundur
dapat dirumuskan dengan :

3. Selisih Pusat
dapat dirumuskan dengan :
$f'(x_0)=\frac{f(x_0 + h) - f(x_0 - h) }{2h}$
Pendekatan di atas dapat digunakan untuk mendapatkan turun pertama. sedangkan untuk mendapatkan turunan kedua dapat di rumuskan :
selisih maju
$f''(x_0)=\frac{f_2 - 2f_{1}+f_0}{h^2}$

Minggu, 18 Desember 2016

Analisis Kesalahan (Error Analysis) Metode Numerik

Secara umum terdapat dua sumber utama penyebab kesalahan dalam perhitangan numerik :

1. Kesalahan Pemotongan (Truncation error)

Kesalahan Pemotongan mengacu pada kesalahan yang ditimbulkan akibat penggunaan hampiran sebagai formula eksak. misalnya, ekspresi matematik yang lebih kompleks di ganti dengan dengan formula yang lebih sederhana.

$R_n(x) = \frac{x - x_0^{(n+1)}}{(n+1)} f^{n+1}(c) , x_0 < c<x$
di sebut galat sisa.

2. Kesalahan Pembulatan (round-off error)
Kesalahan komputer dalam menyajikan bilangan riil menghasilkan galat (kesalahan) yang disebut galat pembulatan. sebagai contoh 1/6 = 0.1666666... tidak dapat dinyatakan secara tepat oleh komputer karena digit 6 panjangnya terbatas.
Angka Bena
Angka Bena adalah adalah angka bermakna, angka penting, atau angka yang dapat di gunakan dengan pasti.
contohnya :
43.123 memiliki 5 angka bena yaitu (4, 3, 1, 2, 3)
0.0090 memiliki 2 angka bena yaitu ( 9, 0)
0.00000012 memiliki 2 angka bena yaitu ( 1, 2)
270.0090 memiliki 7 angka bena yaitu ( 2, 7, 0, 0, 0, 9, 0)
angka 0 bisa menjadi angka bena atau bukan tergantung pada letaknya.
contoh lainnya
$4.3123 \times 10^{1}$ memiliki 5 angka bena

$1.764 \times 10^{-1}$ memiliki 4 angka bena

$1.5 \times 10^{7}$ memiliki 6 angka bena

Kesalahan Mutlak dan Kesalahan Relatif
Definisi
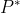
Misalkan $P^{*}$ adalah nilai yang digunakan untuk mengaproksimasi nilai eksak p maka dua macam kesalahan berikut sering digunakan dalam mengukur kualitas aproksimasi, yaitu :

Kesalahan Mutlak (E) = $|p^{*} - p|$
Kesalahan Relatif (R) = $\frac{|p^{*} - p|}{|P|}$